Digital Audio by the numbers
Continued from page 1 ...
So we have discovered that with more switches we can count bigger numbers. Nice. So what? Well what if those switches were the bits in an audio file? Ahhh. The plot thickens.
A Thought Experiment
Just for discussion lets imagine we have a computer that can work with 8 bits at a time. It's connected to an analog to digital interface unit with one input. The input has a microphone plugged into it. Now this interface unit takes a sample of the audio 48,000 times every second and it converts the analog voltage from the microphone into a digital number. With these 8 bit numbers it records 8 bits, with every sample it takes, onto a disk file. The numbers in the file are all recorded in order, exactly as the digitizer got them from the microphone.
Quick how many audio levels can we digitize with 8 bits? (Hint: A bit is just like a switches we talked about on page 1)
Answer: 2 to the power of 8
= 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256 levels of audio!
So that would mean what for audio quality? Well the sample rate is fast enough at 48,000/sec right? So we can accurately record frequencies right up to 20,000 Hz by sampling that fast. So that's good right? But what is the difference between the loudest sound we could record and the quietest sound? In other words the "Dynamic range" (Math alert! math alert! )
Answer :
db = 20Log(voltage1/voltage2)
= 20 x log( 256 / 1 ) = 48dB (That thucks Bevis!)
So 48dB is the **Maximum dynamic range that you could encode with 8 bits. Not very good for audio. So now you get why CDs use 16 bits per sample.
** Note: Well there is a way to make it better with 8 bits but it is (was) used for telephones not recording. See mu-Law encoding if you are interested.
If this makes you dizzy don't worry. The table below does all the math for you. The table shows how things improve when you uses more "switches" ... I mean bits.
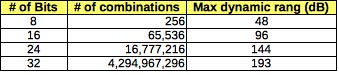
Wow! Look at how the range explodes as the number of bits goes up. This is the power of "exponential math". Everytime you add a bit you double the numeric capability of the encoding system. Doubling means 6 dB more range in the analog signals you can encode.
So it is clear to see that with 24 bits we get a recording system that exceeds the dynamic range of the best analog audio preamps made. And we can see that 16 bits is pretty good but not as wide a recording range as the best audio gear. And it looks like 32 bits would exceed the dynamic range of the human ear and all loudspeakers by a considerable amount.

When I compare 24 bit Audio with a 144dB range from Full scale down to the dithering noise, to the a Studer A80, shown above I am amazed. The A80 was one of the finest tape decks ever made.
It had a range between the noise floor and tape saturation (3% distortion!) of ONLY *61dB!!!
I am soooooo happy that we use digitial audio these days.
